前言
人如何理解单词的含义?
自然语言是活着的语言,同样的词汇和句子在不同上下文情景中可能有不同的含义。同样的话,在不同场合,由不同的人说出来的,也可能是不同的意思。 现在说出的话,与过去或未来,由同一个人说出的相同的话,也可能有完全不同的含义。
日常生活中我们会接触到一些典型的自然语言处理问题解决方案,比如已经普及的机器翻译,office 套件的自动纠错。不久前更是出现了 ChatGPT 这种 颠覆性的产品,完全推翻了我们对传统 chat bot 的印象。
近些年,具有突破性、颠覆性的人工智能产品层出不穷,大模型更是已经成了潮流标配。每个互联网大厂都在跟大模型的风,就算是为了抬升股价,也得 硬着头皮声称在进行 AI 应用的研究。
个人对 NLP 非常、非常感兴趣,应该说是从小就对 AI 非常感兴趣,想法非常多。
因此读书笔记里可能出现一些未经验证的个人想法,我尽量将这些个人想法标出来,以示区别。当然,读书笔记本身是很私人的东西,我不打算也不要求 自己的每行字都必须有凭据可以依靠,或者符合某个标准、主流看法。
但我的确是初入此门,思而不学则殆,所以也会克制对个人想法的表达(应该也不会有什么机会,毕竟是读书为主)。
词处理
自然语言处理的基础是词汇处理,也就是先理解单词的含义。单词是自然语言的最小单位。
最直观的一个问题是,人如何理解单词的含义?我们从小就接触过新华字典,新华字典对字(词)的解释方式是字形、字音、字的含义三要素,我们对机器 的要求是理解字的含义,例如车这个词,我们会给出定义:
1.陆地上有轮子的运输工具:火~。汽~。马~。一辆~。
2.利用轮轴旋转的机具:纺~。滑~。水~。
3.指机器:开~。~间。
4.车削:~圆。~螺丝钉。
5.用水车取水:~水。
6.转动(多指身体):~过身来。
7.姓。
看的出这个词在不同上下文语境有着不同的含义,通过查询词典,我们就知道了火车、汽车、马车,都是一种有轮子的运输工具。类似于人类使用字典, NLP(自然语言处理)领域也有类似的解决方案,叫同义词词典(thesaurus)。
同义词词典的基本内容包括同义词的定义,比如 car 的同义词包括 automobile,machine,motorcar 等。有些词典还会定义词的上位-下位 关系,比如 motorcar 的上位词是 car,即 motorcar 是一种 car 。就像 教科书 是一种 书,语文书 又属于一种 教科书。
同义词词典有个明显的问题,即并不能很好地解决单词的语义,例如:“我要开车了。”,这个车指的是有轮子的运输工具,还是缝纫机、车床,在某些语境 下,“车”还表示折扣商品、带颜色的音像制品等。
以最近折磨我的几个招聘 app 为例,例如我想要找一份 Golang 研发工程师的工作,如果蠢蠢地认为找 Java 方向的工作和找 Go 方向的工作是一回事,就会推 一堆 Java 相关的岗位,非常搞笑而且浪费我时间。如果这些 App 还真就用了一些 NLP 技术,分析了简历,再给出这样的推荐,就更加离谱且搞笑了。
此外还有一些问题,比如维护成本极高(因为整个词典都需要人工定义),还有人力维护肯定没法跟上时代发展。
这时候我们就需要结合上下文,来解决这个问题。
基于计数的方法
更近一点的方法是基于计数(统计)的方法,基本思路是统计词出现在句子中的位置/次数,来确定词的含义。
比如,“我到__去”、“__的特产是......”、“我是____人...”等,经常同时在这些下划线出现的词,就比较可能是较接近的含义。 由此,可以得到一个具有丰富上下文信息的词表示,它记录了这个词在不同上下文中出现的频率,比同义词词典具有更丰富的信息量,而且仅需提供语料库 (经过筛选的文本素材),即可得到一个相对精确的词表示,维护成本要低得多。
关于语料库,NLP 中使用的语料库有事会给文本添加额外的标注信息,比如词性,为此将语料库组织成结构化表示。深度学习进阶这本书的语料库则没有这些 标注信息,就是纯文本。
下面我们看如何实现这个方法。
import re
from typing import List
def preprocess(text: str) -> List[str]:
""" 语料预处理 (注意针对的是英文语料,分词很好做。中文分词又是另一个大问题)
"""
return list(filter(lambda s: len(s) > 0, re.split(r'\W+', text.lower())))
preprocess('I am a student. You are a teacher.')
['i', 'am', 'a', 'student', 'you', 'are', 'a', 'teacher']
PS:这里的 preprocessing 写法和书里的不一样,书中分词后的例子是包含 '.' 这种符号的,我这里写的 preprocessing 不包含符号。
这里我们对语料完成了分词,接下来可以进行统计,但在统计前,为了便于书后续共现矩阵相关内容讲解,我们还要将单词转换成单个整数表示的形式。 方法很简单,每个词第一次出现的时候安排一个自增 ID 即可。我们把所有词丢进一个大字典即可。
import numpy as np
from typing import Dict
def process_word(i2w: Dict[int, str], w2i: Dict[str, int], word: str) -> int:
if word not in w2i:
wid = len(w2i)
i2w[wid] = word
w2i[word] = wid
return wid
else:
return w2i[word]
word_to_id = {}
id_to_word = {}
words = preprocess('I am a student. You are a teacher.')
for w in words:
process_word(id_to_word, word_to_id, w)
print(word_to_id)
corpus = [word_to_id[w] for w in words]
print(np.array(corpus))
{'i': 0, 'am': 1, 'a': 2, 'student': 3, 'you': 4, 'are': 5, 'teacher': 6}
[0 1 2 3 4 5 2 6]
到这里,我们将输入的语料转换成了整数表示形式。将这些功能合并到预处理函数中,得到一个将文本语料库转为整数表示、分好词的 numpy 向量。
import numpy as np
import re
from typing import Dict
def preprocess(text: str):
w2i = {}
i2w = {}
corpus = []
words = list(filter(lambda s: len(s) > 0, re.split(r'\W+', text.lower())))
for word in words:
if word not in w2i:
wid = len(w2i)
i2w[wid] = word
w2i[word] = wid
else:
wid = w2i[word]
corpus.append(wid)
return np.array(corpus), w2i, i2w
corpus, word_to_id, id_to_word = preprocess('I am a student. You are a teacher.')
print(corpus)
[0 1 2 3 4 5 2 6]
现在,基于计数的方法,我们准备将单词表示为向量的形式,在 NLP 领域也叫单词的分布式表示。
NLP 领域有一个分布式假设,单词的含义由其上下文决定。这与我们前面说的同义词词典时提到的问题不谋而合。 而上下文,我们指的是这个单词(关注词)前后的若干个单词。 其中若干个,我们具体选择的数量,称为窗口大小。
选择窗口大小为1,则上下文为关注词的前一个单词和后一个单词,以此类推,称为上下文窗口。 具体实践中,也可以考虑选择仅取左侧单词,或右侧单词为上下文。
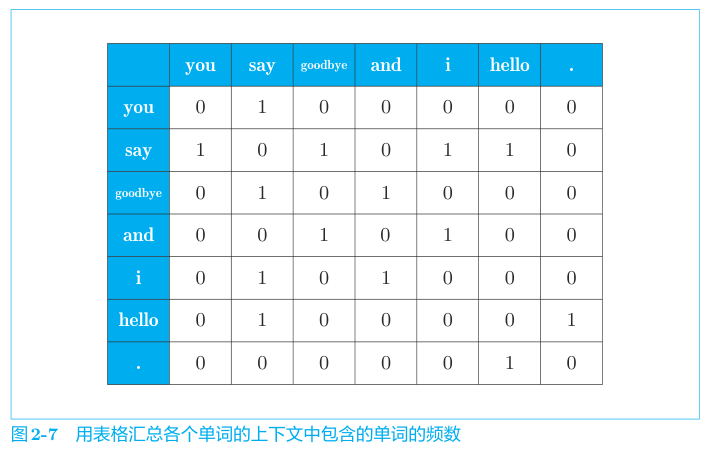
我们可以统计窗口内单词的出现频率,来构造单词的向量表示,然后将所有单词的向量表示汇总成一个矩阵,称为共现矩阵。
共现矩阵的行列均是单词 ID,一行表示一个单词向量,向量的每个元素表示这个单词出现在对应列单词上下文中的次数。比如语料库 包含 you say hello,ID 是 0,1,2 ,则 you 是第一行(下标0),内容是 0,1,0,即 you 在 say 的上下文出现一次。 而 say 就是 1,0,1,即 say 分别在 you 和 hello 的上下文各出现一次。
我们看书中的例子。

最终汇总得到矩阵:
我们尝试用 python 实现这个构造向量、汇总矩阵的过程。
def create_co_matrix(corpus: np.ndarray, vocab_size: int, window_size: int = 1) -> np.ndarray:
""" 构造共现矩阵
corpus: 语料库的向量表示
vocab_size: 词汇表大小
window_size: 窗口大小
"""
co_matrix = np.zeros((vocab_size, vocab_size), dtype=np.int32)
for idx, w in enumerate(corpus):
neighbors = np.concatenate([corpus[max(idx - window_size, 0):idx], corpus[idx + 1:idx + window_size + 1]])
for n in neighbors:
co_matrix[w, n] += 1 # 第 w 行,第 n 列,计数+1
return co_matrix
corpus, word_to_id, id_to_word = preprocess('You say hello and I say goodbye.')
co_matrix = create_co_matrix(corpus, len(word_to_id))
print(co_matrix)
[[0 1 0 0 0 0]
[1 0 1 0 1 1]
[0 1 0 1 0 0]
[0 0 1 0 1 0]
[0 1 0 1 0 0]
[0 1 0 0 0 0]]
现在,我们得到了语料库中每个单词的向量表示,以及单词向量组成的共现矩阵。 下一个问题是,我们如何从单词向量,来评估单词间的相似度呢?
既然单词向量是一个向量,我们自然是用测量向量相似度的方法来评估单词间的相似度。 这里使用余弦相似度算法。
这里给出余弦相似度的公式。
$$ \begin{aligned} similarity(x,y) &= \frac{x \cdot y}{\Vert x \Vert \Vert y \Vert} \\ &= \frac{\sum_{i=1}^{n} x_{i} \times y_{i}}{\sqrt{\sum_{i=1}^{n} (x_{i})^2} \times \sqrt{\sum_{i=1}^{n} (y_{i})^2}} \end{aligned} $$
公式中,分子是两个向量的内积,分母是两个向量的范数之积。
直观地看公式,内积在这里指的就是两个向量的点积(dot product),范数就是向量的长度或者模(modulus)。 但内积和范数又不只是点积和模,作为初学者我不理解为什么书中表述余弦相似度公式时采用这个说法,但继续纠结这个说法有何深意无助于书本当前章节内容的理解。 或许以后遇到相关问题的时候才能意识到这一表述的深意。
因此关于“内积”和“范数”出现在这里的原因以及对应的概念解释,这里不会继续纠缠不清。 但作为零基础学习的一部分,还是需要提一下计算过程。
内积的计算过程: $x \cdot y = \sum_{i=1}^{n} x_{i} \times y_{i}$
范数的计算过程: $\Vert x \Vert = \sqrt{\sum_{i=1}^{n} (x_{i})^2}$
以及余弦相似度公式本身的含义:求两个向量的夹角余弦值。
推导过程非常简单,欧氏空间的点积公式是:$a \cdot b = \Vert a \Vert \Vert b \Vert \cos \theta$
很容易就能得到 $\cos \theta = \frac{a \cdot b}{\Vert a \Vert \Vert b \Vert}$
这里给出一些我在读这几行文字的时候,搜索到的资料:
余弦相似度公式对向量的长度不敏感,因此语料库中两个含义相似的词(上下文相似),即使其中一者出现的频率较低,依然可以判断为相似。
我们用 python 实现一下余弦相似度算法。
def cosine_similarity(x: np.ndarray, y: np.ndarray, *, eps=1e-8) -> float:
""" 计算余弦相似度
x, y: 向量
"""
assert len(x) == len(y)
return (np.dot(x, y)) / (np.linalg.norm(x) * np.linalg.norm(y) + eps)
you_id = word_to_id['you']
i_id = word_to_id['i']
y = cosine_similarity(co_matrix[you_id], co_matrix[i_id])
print(y)
0.7071067761865475
与书中计算结果接近,都是 0.7 左右。
现在有了词向量和相似度计算公式,我们可以给定一个词,查找与其最接近的词(或词列表)。
from typing import Optional
def most_similar(query: str, word_to_id: dict, id_to_word: dict, word_matrix: np.ndarray, top: int = 5) -> Optional[
List[str]]:
if query not in word_to_id:
print(f'没有 {query} 这个单词')
return
query_id = word_to_id[query]
vocab_size = len(word_to_id)
similarity = np.zeros(vocab_size)
for i in range(vocab_size):
similarity[i] = cosine_similarity(word_matrix[query_id], word_matrix[i])
for idx, i in enumerate((-similarity).argsort()):
word = id_to_word[i]
print(idx, word, similarity[i])
most_similar('you', word_to_id, id_to_word, co_matrix)
0 you 0.9999999900000002
1 goodbye 0.9999999900000002
2 hello 0.7071067761865475
3 i 0.7071067761865475
4 say 0.0
5 and 0.0
注意到输出和书中不同,因为书中的 preprocess 结果包含一个 . ,而我们这里的 preprocess 结果不包含。 因此在 goodbye 这个单词上,上下文和 you 一样只包含 say,向量表示也一样,因此相似度是最高的。 书中的 goodbye 有个额外的上下文 . ,相似度就低了。
相信有人已经注意到了,这里统计单词出现频次的方法有很多问题。上下文中单词出现的位置和顺序,和单词的含义是有很大关系的。 举个粗俗的例子来说,飞机打我和我打飞机是完全的两码事!
有经验的程序员应该在读到创建共现矩阵这一步的时候就立刻注意到,共现矩阵的空间复杂度是多项式级别的 $O(n^2)$,而查询 同义词的时间复杂度是 $O(n)$,这在语料库非常大的情况下,会带来非常严重的性能问题。
此外,就连单词向量表示方法也存在很大问题。对于一些常用冠词、介词,它们的含义和上下文没有关系,但因为经常出现而被认为 和上下文存在强相关。
对于向量表示方法的问题,书中引入了 点互信息 (PMI,Pointwise Mutual Information)来处理。
PMI 函数定义为:$PMI(x,y) = \log_2 \frac{P(x,y)}{P(x)P(y)}$
其中,$P(x)$ 表示 x 发生的概率,$P(y)$ 表示 y 发生的概率,$P(x,y)$ 表示 x 和 y 同时发生概率。PMI的值越高,两个词的相关性越强。
为了计算 $P(x)$ 我们定义 $C$ 为共现矩阵, $C(x)$ 为 x 在共现矩阵中出现的次数,$C(x,y)$ 则是 x 和 y 同时发生的次数(x上下文中出现y的次数加上y的上下文中出现x的次数)。 定义 N 为所有单词出现的次数之和(同样是共现矩阵中的)。
得到公式:$PMI(x,y) = \log_2 \frac{C(x,y) \cdot N}{C(x) \cdot C(y)}$
这里有个迷惑的问题,就是为什么要计算共现矩阵中 x 和 y 以及 x,y 出现的次数,而不是语料库中出现的次数? 另外 PMI 本身,是一个源自概率论/信息学的概念,和余弦相似度里范数、内积这些数学领域的内容一样暂不讨论。
再进一步,当共现次数为0时(即 $C(x,y)=0$),PMI会得到 $-\infty$,这不好。对于负的 PMI 我们做一个 ReLU 式的处理,得到新的函数 $PPMI(x,y) = \max(0, PMI(x,y))$
当 $PMI(x,y)<0$ ,$PPMI(x,y)$ 得到 0。
接着还是用 python 实现一下求 ppmi 的函数。
PS: 为了方便验证实现,我接下来会用书中的 preprocess 函数,而不是我自己定义的。
from common.util import preprocess, create_co_matrix
from rich.console import Console
from rich.table import Table
corpus, word_to_id, id_to_word = preprocess('You say hello and I say goodbye.')
co_matrix = create_co_matrix(corpus, len(word_to_id))
def _pretty_print_covariance_table(C: np.ndarray, *, title='covariance table') -> None:
console = Console()
covariance_table = Table(title=title)
covariance_table.add_column('/')
for i in range(C.shape[0]):
covariance_table.add_column(id_to_word[i])
for i in range(C.shape[0]):
covariance_table.add_row(id_to_word[i], *[str(C[i, j]) for j in range(C.shape[1])])
console.print(covariance_table)
def ppmi(C: np.ndarray, verbose: bool = False, eps: float = 1e-8) -> np.ndarray:
_pretty_print_covariance_table(C)
M = np.zeros_like(C, dtype=np.float32) # 新的 PPMI 矩阵
N = np.sum(C) # 所有单词出现的总次数
S = np.sum(C, axis=0) # 单独计算某个单词出现的次数
# 查看每个单词在共现矩阵出现的次数
# 这个计数实际算的是单词出现在其他单词上下文中的次数。比如 you say hello
# say 这个词在语料库里只出现一次,但在共现矩阵里计数是 2 次,分别在 you 的上下文和 hello 的上下文里出现 1 次。
console = Console()
table = Table(title='word count')
table.add_column('word')
table.add_column('count')
for i in range(len(S)):
table.add_row(id_to_word[i], str(S[i]))
console.print(table)
total = C.shape[0] * C.shape[1] # 矩阵大小,方便在大语料库处理时计算和观察进度用
cnt = 0 # 当前处理到的位置
# 遍历共现矩阵的行
for i in range(C.shape[0]):
# 遍历共现矩阵的列
for j in range(C.shape[1]):
# C[i,j] 取单词 i 上下文中 j 出现的次数,即 C(i,j)
# S[i],S[j] 取单词 i,j 分别在共现矩阵出现的总次数,即 C(i) 和 C(j)
# eps 微小值避免 C(i,j) 为 0 的情况下,求 log2(0) 得到 -inf 的结果。
# 至少在 C(i,j) 为 0 的时候可以得到 log2(eps)
pmi = np.log2(C[i, j] * N / (S[i] * S[j]) + eps)
M[i, j] = max(0, pmi)
# 观察进度
cnt += 1
if cnt % 10000 == 0:
if verbose:
print(f'已完成 {cnt / total * 100:.1f}%')
return M
ppmi_co_matrix = ppmi(co_matrix)
_pretty_print_covariance_table(ppmi_co_matrix, title='ppmi covariance table')
covariance table ┏━━━━━━━━━┳━━━━━┳━━━━━┳━━━━━━━┳━━━━━┳━━━┳━━━━━━━━━┳━━━┓ ┃ / ┃ you ┃ say ┃ hello ┃ and ┃ i ┃ goodbye ┃ . ┃ ┡━━━━━━━━━╇━━━━━╇━━━━━╇━━━━━━━╇━━━━━╇━━━╇━━━━━━━━━╇━━━┩ │ you │ 0 │ 1 │ 0 │ 0 │ 0 │ 0 │ 0 │ │ say │ 1 │ 0 │ 1 │ 0 │ 1 │ 1 │ 0 │ │ hello │ 0 │ 1 │ 0 │ 1 │ 0 │ 0 │ 0 │ │ and │ 0 │ 0 │ 1 │ 0 │ 1 │ 0 │ 0 │ │ i │ 0 │ 1 │ 0 │ 1 │ 0 │ 0 │ 0 │ │ goodbye │ 0 │ 1 │ 0 │ 0 │ 0 │ 0 │ 1 │ │ . │ 0 │ 0 │ 0 │ 0 │ 0 │ 1 │ 0 │ └─────────┴─────┴─────┴───────┴─────┴───┴─────────┴───┘
word count ┏━━━━━━━━━┳━━━━━━━┓ ┃ word ┃ count ┃ ┡━━━━━━━━━╇━━━━━━━┩ │ you │ 1 │ │ say │ 4 │ │ hello │ 2 │ │ and │ 2 │ │ i │ 2 │ │ goodbye │ 2 │ │ . │ 1 │ └─────────┴───────┘
ppmi covariance table ┏━━━━━━━━━┳━━━━━━━━━━━┳━━━━━━━━━━━┳━━━━━━━━━━━┳━━━━━━━━━━━┳━━━━━━━━━━━┳━━━━━━━━━━━┳━━━━━━━━━━┓ ┃ / ┃ you ┃ say ┃ hello ┃ and ┃ i ┃ goodbye ┃ . ┃ ┡━━━━━━━━━╇━━━━━━━━━━━╇━━━━━━━━━━━╇━━━━━━━━━━━╇━━━━━━━━━━━╇━━━━━━━━━━━╇━━━━━━━━━━━╇━━━━━━━━━━┩ │ you │ 0.0 │ 1.8073549 │ 0.0 │ 0.0 │ 0.0 │ 0.0 │ 0.0 │ │ say │ 1.8073549 │ 0.0 │ 0.8073549 │ 0.0 │ 0.8073549 │ 0.8073549 │ 0.0 │ │ hello │ 0.0 │ 0.8073549 │ 0.0 │ 1.8073549 │ 0.0 │ 0.0 │ 0.0 │ │ and │ 0.0 │ 0.0 │ 1.8073549 │ 0.0 │ 1.8073549 │ 0.0 │ 0.0 │ │ i │ 0.0 │ 0.8073549 │ 0.0 │ 1.8073549 │ 0.0 │ 0.0 │ 0.0 │ │ goodbye │ 0.0 │ 0.8073549 │ 0.0 │ 0.0 │ 0.0 │ 0.0 │ 2.807355 │ │ . │ 0.0 │ 0.0 │ 0.0 │ 0.0 │ 0.0 │ 2.807355 │ 0.0 │ └─────────┴───────────┴───────────┴───────────┴───────────┴───────────┴───────────┴──────────┘
PPMI 矩阵依然存在一个问题,计算 PPMI 的过程时间复杂度是多项式级别的 $O(n^2)$,存储空间复杂度也是 $O(n^2)$。 语料库非常大的时候,PPMI 计算量和存储空间需求会急剧膨胀。而进一步观察矩阵,会发现这个矩阵的大部分元素都是 0。
PS: 立刻想到了稀疏矩阵的压缩存储。但压缩存储后参与计算就很麻烦了,归根结底这是个计算密集的场景。
书中引入的方法是降维,将矩阵 $C$ 降维到 $k$ 维,得到矩阵 $U$,$U$ 的每一列表示 $C$ 的一个特征向量。在这个场景是 将二维的共现矩阵降维到 1 维,得到一个特征向量,这个特征向量表示了矩阵 $C$ 的一个特征值。
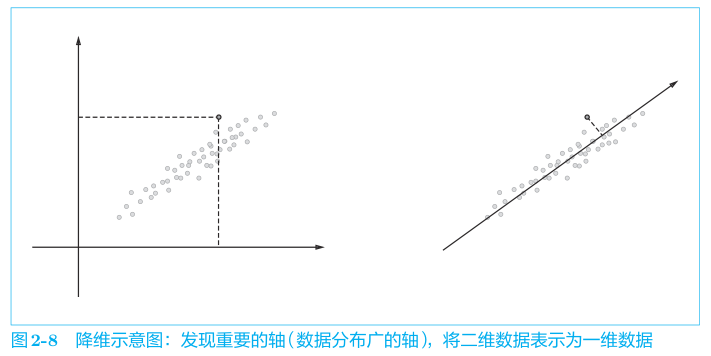
降维的方法是 SVD (奇异值分解,Singular Value Decomposition),将任意矩阵 $X$ 分解成3个矩阵的乘积,定义为 $X=USV^T$
PS: SVD 是什么以及出现在这里的意义又是一个数学领域的问题,我没能力讨论就不废话了。
书中将$USV^T$概括为:
- $U$ 矩阵视作单词空间
- $S$ 视作重要性矩阵,我们裁剪 $S$ 来实现对原矩阵的有损压缩,裁剪 $S$ 的同时要跟着裁剪 $V^T$ 和 $U$
书中的用法是,对例如 1000 个单词的原矩阵 $C_{1000 \times 1000}$,SVD 后截取 $U$ 矩阵的前 N 列,得到降维表示的单词向量。
简单实现一下。
from common.util import preprocess, create_co_matrix, ppmi
text = 'You say hello and i say goodbye.'
corpus, word_to_id, id_to_word = preprocess(text)
C = create_co_matrix(corpus, len(word_to_id))
W = ppmi(C)
U, S, V = np.linalg.svd(ppmi_co_matrix)
np.set_printoptions(precision=3) # 有效位数为3位
print(C[0])
print(W[0])
print(U[0])
[0 1 0 0 0 0 0]
[0. 1.807 0. 0. 0. 0. 0. ]
[-1.110e-16 3.409e-01 -1.205e-01 -4.163e-16 -1.110e-16 -9.323e-01
-2.426e-17]
PS: 书中的输出是这样的
print(U[0]) # SVD[ 3.409e-01 -1.110e-16 -1.205e-01 -4.441e-16 0.000e+00 -9.323e-01 2.226e-16]但实际附带的案例代码,跑出来的结果是上图所示的。不是我写的不对,是书里写的输出有问题。
import matplotlib.pyplot as plt
for word, word_id in word_to_id.items():
plt.annotate(word, (U[word_id, 0], U[word_id, 1]))
plt.scatter(U[:, 0], U[:, 1], alpha=0.5)
plt.show()
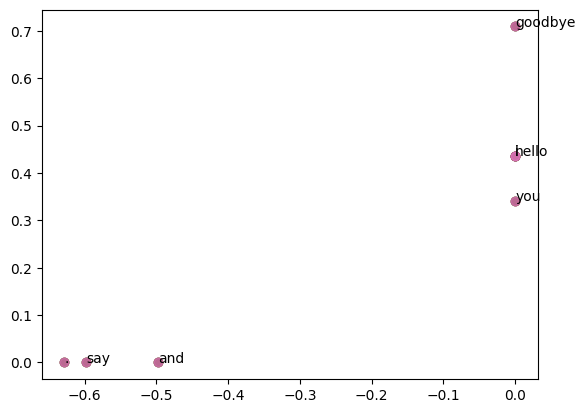
PS: 眼尖的兄弟应该又看出来了,和书里的还是不一样。
SVD 算法的时间复杂度是 $O(n^3)$,书中提到可以用 sklearn 的 TruncatedSVD 算法加速。TruncatedSVD 会丢弃一些较小的奇异值。
PS: 奇异值是什么,还得再回头翻书。
总之,书到这里,我们可以开始在真正的语料库上创建单词向量了。书中使用 Penn Treebank 语料库,这里就跟着做一下实验。
from dataset.ptb import load_data
from common.util import create_co_matrix, ppmi, most_similar
# 结构和我们的 preprocess 一样
corpus, word_to_id, id_to_word = load_data('train')
vocab_size = len(word_to_id)
window_size = 2
wordvec_size = 100
print('[+] 正在创建共现矩阵...')
C = create_co_matrix(corpus, vocab_size, window_size=window_size)
print('[+] 正在计算 PPMI...')
W = ppmi(C, verbose=True)
print('[+] 正在计算 SVD...')
try:
# truncated SVD (fast!)
from sklearn.utils.extmath import randomized_svd
U, S, V = randomized_svd(W, n_components=wordvec_size, n_iter=5, random_state=None)
except ImportError:
U, S, V = np.linalg.svd(W)
print('[+] 词向量计算完成')
word_vecs = U[:, :wordvec_size]
queries = ['you', 'year', 'car', 'toyota']
for query in queries:
most_similar(query, word_to_id, id_to_word, word_vecs)
[+] 正在创建共现矩阵...
[+] 正在计算 PPMI...
F:\repos\DL-NLP\common\util.py:139: RuntimeWarning: overflow encountered in scalar multiply
pmi = np.log2(C[i, j] * N / (S[j]*S[i]) + eps)
F:\repos\DL-NLP\common\util.py:139: RuntimeWarning: invalid value encountered in log2
pmi = np.log2(C[i, j] * N / (S[j]*S[i]) + eps)
1.0% done
2.0% done
3.0% done
4.0% done
5.0% done
6.0% done
7.0% done
8.0% done
9.0% done
10.0% done
11.0% done
12.0% done
13.0% done
14.0% done
15.0% done
16.0% done
17.0% done
18.0% done
19.0% done
20.0% done
21.0% done
22.0% done
23.0% done
24.0% done
25.0% done
26.0% done
27.0% done
28.0% done
29.0% done
30.0% done
31.0% done
32.0% done
33.0% done
34.0% done
35.0% done
36.0% done
37.0% done
38.0% done
39.0% done
40.0% done
41.0% done
42.0% done
43.0% done
44.0% done
45.0% done
46.0% done
47.0% done
48.0% done
49.0% done
50.0% done
51.0% done
52.0% done
53.0% done
54.0% done
55.0% done
56.0% done
57.0% done
58.0% done
59.0% done
60.0% done
61.0% done
62.0% done
63.0% done
64.0% done
65.0% done
66.0% done
67.0% done
68.0% done
69.0% done
70.0% done
71.0% done
72.0% done
73.0% done
74.0% done
75.0% done
76.0% done
77.0% done
78.0% done
79.0% done
80.0% done
81.0% done
82.0% done
83.0% done
84.0% done
85.0% done
86.0% done
87.0% done
88.0% done
89.0% done
90.0% done
91.0% done
92.0% done
93.0% done
94.0% done
95.0% done
96.0% done
97.0% done
98.0% done
99.0% done
[+] 正在计算 SVD...
[+] 词向量计算完成
[query] you
i: 0.6721723079681396
we: 0.6572807431221008
do: 0.5788654685020447
'd: 0.5358506441116333
've: 0.5161784291267395
[query] year
last: 0.6547753810882568
month: 0.6300122141838074
next: 0.6260495781898499
quarter: 0.5872719287872314
february: 0.5810660123825073
[query] car
luxury: 0.6643019914627075
auto: 0.6334719061851501
corsica: 0.5723612308502197
truck: 0.5713587403297424
domestic: 0.5277842283248901
[query] toyota
motor: 0.7351067066192627
nissan: 0.6682652831077576
motors: 0.643950343132019
honda: 0.6137979626655579
lexus: 0.6087179183959961
需注意几个点,上述代码中我们没有用前面解释 pmi 和 共现矩阵时的窗口大小和向量大小,词向量取 100 维,而窗口是 2 不是 1。
这几个参数取值会影响结果,书上代码抄下来结果不一致可以注意下这些细节参数。
总结
这一章涉及很多交叉领域的概念,所以读起来是有点吃力的。本来想直接写 markdown 但发现不用 jupyter 嵌几个示例会很难 说清楚。
遗留的几个问题包括:
- 关于 PPMI/PMI/MI 互信息是个什么鬼,为何可以表示关联性。
- SVD 奇异值分解原理,主要是理解 U 矩阵为什么能表示词空间,矩阵相关的东西很难在学 DL 的时候避开了。
- 内积和范数,这个还好。至少不影响对余弦相似度公式的理解。
再次体会到搞 AI 的话我的基础确实薄弱。