神经网络的学习
概念
深度学习
神经网络的特征是从数据中学习。
显然稍有规模的神经网络,一个一个神经元去设置权重是非常困难的事情。
又好又快地学习到权重就是深度学习的重头戏啦。
然后,学习需要海量的数据,所以数据是深度学习的命根子。
深度学习和传统机器学习技术的区别是传统机器学习过程,需要先由人发现规律(特征),然后用合适的机器学习技术(SVM 支持向量机、KNN 等)学习识别特征。
深度学习则是由神经网络直接吃数据,找出潜在的特征或规律。
数据集
机器学习中一般把数据分为训练集和测试集,训练集就像是靶场专门用来练习改进的,测试集则是考核评估训练结果。训练数据也称为监督数据。
处理未被观察过的数据的能力叫泛化能力。对特定输入集合表现很好但在未知的输入上表现不好叫过拟合。
one-hot 表示
例如识别手写数字的神经网络输出是 10 个浮点数,表示数字 0-9 的概率。
对正确数字的标签我们可以记为下标,即正确数字是 0-9 之间的一个整数。
用 one-hot 表示正确数字的标签,即把正确数字的标签记为 0,其他数字记为 1,这样神经网络的输出就是 10 个浮点数,只有正确数字的那个位置是 1,其他都是 0。
例如正确数字是 2 ,则 one-hot 表示为 [0,0,1,0,0,0,0,0,0,0]。
损失函数
**损失函数 (loss function)**是表示神经网络性能恶劣程度的指标,即神经网络的结果和监督数据有多不拟合。
均方误差
均方误差 (Mean Squared Error, MSE) 就是常用的损失函数。
$$ MSE = \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y_i})^2 $$
import numpy as np
def mean_squared_error(y, t):
""" 均方误差损失函数 """
return 0.5*np.sum((y - t) ** 2)
# softmax 输出
y = np.array([0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0])
# one-hot 表示的正确标签
t = np.array([0, 1, 0, 0, 0, 0, 0, 0, 0, 0])
# 计算均方误差
print(mean_squared_error(y, t))
# softmax 输出
y = np.array([0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0])
# one-hot 表示的正确标签
t = np.array([0, 0, 1, 0, 0, 0, 0, 0, 0, 0])
# 计算均方误差,注意 softmax 在正解位置输出的概率是0.6,更接近 1 了,相应的均方误差也降低了
# 说明和监督数据更接近了
print(mean_squared_error(y, t))
0.6475
0.09750000000000003
交叉熵误差
交叉熵误差公式如下:
$$ E=-\sum_{k} t_k \log_e y_k $$
和均方误差一样,下标 k 表示输出维度,$t_k$ 表示正确解标签(one-hot 表示),$y_k$ 表示预测值。
因为 $t_k$ 在非正确解下标上都是 0,所以实际交叉熵可以化简为下面这样:
$$ E=-log_e y_k $$
其中 k 表示正确解的下标。
交叉熵函数定义和函数图像如下。
import matplotlib.pyplot as plt
import numpy as np
def cross_entropy_error(y, t):
_delta = 1e-7
return -np.sum(np.log(y+_delta)*t)
y = np.array([0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0])
t = np.array([0.0, 0.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0])
print('交叉熵误差', cross_entropy_error(y, t))
x = np.arange(0.01, 1, 0.01)
y = -np.log(x)
plt.plot(x, y)
plt.show()
交叉熵误差 0.510825457099338
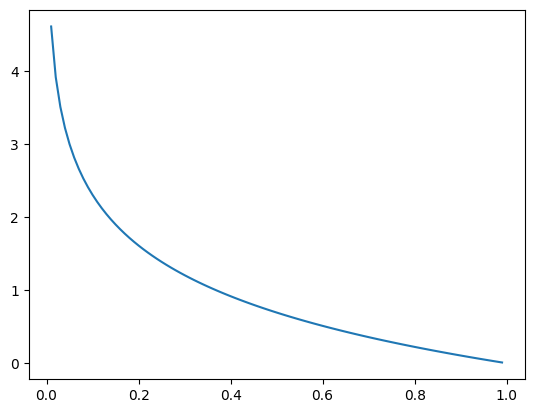
很容易看出来当预测值越接近 0,也就是偏差越大,交叉熵误差的结果就越大。预测值越接近 1,偏差越小,则交叉熵误差结果越小。
mini-batch
因为训练的目的是在整个训练集上表现更好,所以评估损失自然也是基于整个训练集的。
上文的损失函数仅评估了单个样本的损失,实际训练中评估的应该是在训练集上的损失总和。
以交叉熵误差为例,训练集的损失函数应该这样定义:
$$ E=-\frac{1}{n} \sum_{n} \sum_{k}t_{nk} \log_e y_{nk} $$
其中 n 定义为训练集的样本数,下标 nk 表示第 n 个样本输出的第 k 个维度。
$y_{nk}$ 表示第 n 个样本的神经网络输出,$t_{nk}$ 表示第 n 个样本的真实标签。
但也要意识到,以整个训练集的评估结果计算损失成本是比较高的,仅 MNIST 训练集就有 60000 个样本,计算量很大。
mini-batch 的设想是将训练集分成若干个小批量,每个小批量的大小可以根据实际情况调整。
在每个小批量上计算损失,然后将这些损失求和,这样可以大大减小计算量。
注:个人看法,如果训练集很大而且内部的样本差异非常大,mini-batch 抽取的批量 可能很难代表整个训练集,想要保证效果可能就要增加多轮 epoch 迭代才行。选择样本 构造合适的 mini-batch 应该在有些场景下也很重要。
下面是从训练集随机抽取一定数量的样本形成 mini-batch 的方法。
import os
import sys
import numpy as np
def load_mnist(*args, **kwargs):
repo_root = os.path.abspath(os.path.pardir)
if repo_root not in sys.path:
sys.path.append(repo_root)
from dataset.mnist import load_mnist
return load_mnist(*args,**kwargs)
def mini_batch(training_data, labels, batch_size):
""" 在数据集中随机抽取 mini-batch
"""
print(training_data.shape)
mask = np.random.choice(training_data.shape[0], batch_size)
return training_data[mask], labels[mask]
# mini-batch 大小
batch_size = 100
# 总训练集和测试集
(x_train, t_train), (x_test, t_test) = load_mnist(one_hot_label=True)
# 抽取 mini-batch
x_batch, t_batch = mini_batch(x_train, t_train, batch_size)
print(f'训练集 {x_batch.shape} 标签 {t_batch.shape}')
def cross_entropy_error(y, t):
# 对于单个样本输入(即输入 y 是个向量)则先转成一维的矩阵,再按公式计算交叉熵损失。
""" 交叉熵损失函数 """
if y.ndim == 1 and t.ndim == 1:
t = t.reshape(1, t.size)
y = y.reshape(1, y.size)
# 计算这个 mini-batch 的交叉熵损失
#
# 按照第三章批量计算的公式,输入是二维矩阵的时候,输出也是二维矩阵,输出的行表示样本,列表示类别。
#
# 因此可以得知 y 和 t 应该都是 (batch_size, 10) 的矩阵,用 element-wise 方式计算 t - log(y) 得到
# (batch_size, 10) 的交叉熵结果矩阵。理解的重点在 t * np.log(y + delta) 的参数计算过程是 element-wise 的。
#
# 理解了这一点,-np.sum()/y.shape[0] 就很好理解了。
# 矩阵所有元素求和得到 mini-batch 的综合损失,除以样本数得到平均每个样本的交叉熵损失。
delta = 1e-7
return -np.sum(t * np.log(y + delta)) / y.shape[0]
# 测试计算单个样本的交叉熵损失
p = np.array([0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0])
t = np.array([0, 0, 1, 0, 0, 0, 0, 0, 0, 0])
loss = cross_entropy_error(p, t)
print(loss)
# 测试计算 mini-batch 的交叉熵损失
p = np.array([[0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0],
[0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]])
t = np.array([[0, 0, 1, 0, 0, 0, 0, 0, 0, 0],
[0, 1, 0, 0, 0, 0, 0, 0, 0, 0]])
loss = cross_entropy_error(p, t)
print(loss)
(60000, 784)
训练集 (100, 784) 标签 (100, 10)
0.510825457099338
1.7532778653276644
此处解释一下 mini_batch 函数的原理。
np.random.choice 作用是从指定的数组随机抽取 n 个元素,首个参数是待抽取的数组,第二个参数是抽取的数量。 但这里传递的首参数 a 是一个 int 型整数,这个情况下 np.random.choice 的行为会变成在 np.arange(0, a) 范围内抽取 n 个元素。 所以,这里实际抽取到的是小批量样本的下标。
然后就是 numpy 数组的另一个特性,支持数组下标索引。 换言之,我们可以以序列类型传递多个下标给 __getitem__ 魔术方法,传递下标序列时会返回多个元素。
书中另一种小批量交叉熵损失计算方式仅仅是另一种形式获取预测结果以计算 $\sum_{k} \log_e y_k$ ,并没有太大差异,就不赘述了。
下面简单演示下 numpy 数组的下标特性用法。
import numpy as np
arr = np.array([1, 2, 3, 4, 5])
print(f'数组是 {arr}')
idx = 0
print(f'通常下标 arr[{idx}] 访问: {arr[0]}')
idx = [0, 1, 2]
print(f'多个下标 arr[{idx}] 访问: {arr[idx]}')
# 多维数组也支持这个用法,多维数组指定多个下标的时候索引序列的元素是被索引的元素下标序列
arr = np.array([[1,2,3,4,5],[1,2,3,4,5],[1,2,3,4,5]])
print(f'数组是 {arr}')
# 多维数组下标有个特点是需要用 tuple 作为索引类型,索引语法是 arr[dim1,dim2,...,dimN],每个 dim 都是待索引元素在该维度的下标序列
idx = ([0, 0, 0], [0, 1, 2])
print(f'多维数组多个下标 arr[{idx}] 访问: {arr[idx]}')
数组是 [1 2 3 4 5]
通常下标 arr[0] 访问: 1
多个下标 arr[[0, 1, 2]] 访问: [1 2 3]
数组是 [[1 2 3 4 5]
[1 2 3 4 5]
[1 2 3 4 5]]
多维数组多个下标 arr[([0, 0, 0], [0, 1, 2])] 访问: [1 2 3]
损失函数的意义
损失函数的作用是衡量预测结果与真实结果的差距,从而得到模型的预测结果。
在书中,作者说不能使用识别精度为依据进行训练,其实原因和阶跃函数那一节差不多。
作者书中举例的精度定义是 精确度=正确数/总样本数,因为正确数和样本数都是整数,精确度其实是离散的点。 换句话说,用精确度来计算就像是问你猜猜看我脑子里在想的是哪个数,你说 1,我说不对,你说 2,我说不对...神经网络无法从训练反馈的结果得知调整有没有作用,就像是在一个无限大的无序集合里搜索一个数,什么时候能找到全看运气。 而损失函数在这个游戏里就是,我问你我在想哪个数,你说 1,我说大概 30%正确;你说 2,我说大概 50%正确;你说 3,我说大概 70%正确...训练神经网络时就知道往这个方向调整是在逼近正确答案了。
上面这个例子换成数学概念就是导数,即略微改变输入参数,函数输出会产生多大的改变。放到函数图形里就是斜率,得到斜率也就知道了往哪个方向调整可以降低损失。
注:如果发现权重往大或者往小微调都会增加损失,并不一定代表权重已经处于最优,也可能卡在半山腰呢。
如果以精确度计,那函数图像里大部分地方都是平行于 x 轴的,斜率为 0。精确度函数是个阶跃函数。微调参数很难直接影响精确度。当然非要杠一下把精确度定义成接近正确的程度(就是$-loss()$嘛)也行,就是给损失函数换了个说法而已。
数值微分
又到了考验我可怜的数学水平的时候了,别人是半桶水我大概是个空瓶。
这一节主要讲导数的概念,导数定义如下:
$$ \frac{d}{dx} f(x) = \lim_{h \to 0} \frac{f(x + h) - f(x)}{h} $$
公式中 $h$ 表示一个小的变化量,$f(x)$ 表示函数在 $x$ 处的值,$f(x + h)$ 表示函数在 $x$ 处加上 $h$ 后的值,$\frac{f(x + h) - f(x)}{h}$ 表示这个小变化量对函数值的影响。。
加上 $\lim_{h \to 0}$ 之后,这个公式表示的就是一个极小的变化量对函数值的影响。
注:高中知识,函数图像上一点的切线斜率就是导数。
导数在数学公式里可以写成一撇,比如 $(e^x)'=e^x$ 。
导数公式不能直接套用到 python 实现:
- 显然你没有一个标量 h 可以代入。
- 即使选择一个足够小的 h 值,避免了舍入误差,实际计算的也是 $f(x + h)$ 和 $f(x)$ 之间的导数,而不是 $f(x)$ 这一点的导数。
只能求近似,方法是计算 $\frac{f(x+h)-(x-h)}{2h}$,也就是 $f(x+h)$ 到 $f(x-h)$ 之间的导数均值。书中叫 中心差分。$f(x+h)-f(x)$ 叫前向差分。
利用微小的差分求导数的过程称为数值微分(numerical differentiation),求得的导数是对解析解的近似,也叫数值解。
基于数学式推导求导数的过程叫 解析性求导,求得的导数是无误差的 解析解。
数值微分求导的 python 代码实现如下:
from typing import Callable, Union
import matplotlib.pyplot as plt
import numpy as np
def numerical_diff(f: Callable[[float], float], x: float):
h = 1e-4 # 0.0001
return (f(x+h) - f(x-h)) / (2*h)
def f(x: Union[float, np.ndarray]) -> Union[np.ndarray, float]:
""" 测试求导的函数 """
return 0.01*x**2+0.1*x
# 绘制函数图像
x = np.arange(0, 20, 0.1)
y = f(x)
plt.xlabel('x')
plt.ylabel('f(x)')
plt.plot(x, y)
plt.show()
# 求导 x=5 和 x=10
print('x=5 时 f 的导数近似为', numerical_diff(f, 5))
print('x=5 时 f 的导数近似为', numerical_diff(f, 10))

x=5 时 f 的导数近似为 0.1999999999990898
x=5 时 f 的导数近似为 0.2999999999986347
多个参数的函数的导数称为 偏导数 。
然后是对于有多个参数的函数求导,比如 $f(x,y)=x^2+y^2$ 在 $x=4,y=5$ 处的导数, 做法是先求 $f(x,y)$ 在 $x$ 处的偏导数,然后求 $f(x,y)$ 在 $y$ 处的偏导数(先后无关)。
def f2(x,y):
return x**2+y**2
# d1,d2 就是 f2 的偏导数了
d1 = numerical_diff(lambda x:f2(x,4),3)
d2 = numerical_diff(lambda y:f2(3,y),4)
偏导数的数学表达:$\frac{\partial f}{\partial x}$ 表示 $f(x,y)$ 函数关于 $x$ 的偏导数。
此外还有一些常见基本初等函数的求导公式找本高数书应该都有写。
梯度
由全部变量的偏导数汇总而成的向量叫梯度,以 $f(x,y)=x^2+y^2$ 为例,梯度公式为:$(\frac{\partial f}{\partial x},\frac{\partial f}{\partial y})$
梯度计算的 python 实现如下。
from typing import Callable
import matplotlib.pyplot as plt
import numpy as np
from matplotlib import cm
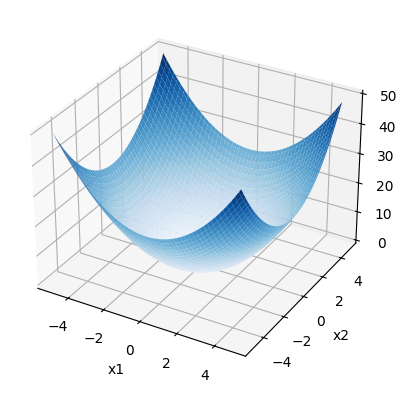
def f(x):
return x[0]**2 + x[1]**2
# 绘制函数图像
fig, ax = plt.subplots(subplot_kw={"projection": "3d"})
x1 = np.arange(-5, 5, 0.1)
x2 = x1.copy()
x1, x2 = np.meshgrid(x1, x2)
y = f(np.array([x1, x2]))
ax.plot_surface(x1, x2, y, cmap=cm.Blues)
ax.set_xlabel('x1')
ax.set_ylabel('x2')
ax.set_zlabel('y')
plt.show()
def numerical_gradient(f: Callable[[np.ndarray], np.ndarray], x: np.ndarray):
""" 数值微分法计算梯度
注意输入的 np.ndarray 输入的维度是一维,但也可以是多维。函数实现中基本是 element-wise 的运算
"""
h = 1e-4 # 0.0001
grad = np.zeros_like(x) # 生成和输入参数形状一致的数组
for idx in range(x.size):
tmp_val = x[idx]
# 公式中 f(x+h) 的部分
x[idx] = tmp_val+h
fxh1 = f(x)
# 公式中 f(x-h) 的部分
x[idx] = tmp_val-h
fxh2 = f(x)
# 公式主体部分 f(x+h)-f(x-h)/2h
grad[idx] = (fxh1-fxh2)/(h*2)
# 还原输入 x,计算下一个维度的偏导数
x[idx] = tmp_val
return grad
# 单个点的梯度
grad = numerical_gradient(f, np.array([3.0, 4.0]))
print(f'单个点的梯度:{grad}')
单个点的梯度:[6. 8.]
接着尝试将梯度图形化绘制。
基本思路是:
- 取 x1,x2 范围为 -5 到 5 之间
- 网格化 x1,x2,获得两个二维数组 x1', x2',分别表示 x 轴坐标和 y 轴坐标,形成一个网格。
- 扁平化二维数组,得到两个一维数组。
- 以两个一维数组组成输入,计算梯度,得到网格上每个点的梯度。
- 绘制梯度向量。
# 计算区间 0-5,0-5 区间的梯度,绘制网格
x1 = np.arange(-5, 5, 1.0)
x2 = np.arange(-5, 5, 1.0)
m1, m2 = np.meshgrid(x1, x2)
x1 = m1.flatten()
x2 = m2.flatten()
grad = numerical_gradient(f, np.array([x1, x2]))
# 绘制图
plt.quiver(x1, x2, -grad[0], -grad[1])
plt.show()
# 梯度向量图
fig, ax = plt.subplots(subplot_kw={"projection": "3d"})
y = f(np.array([x1, x2]))
y = np.reshape(y, m1.shape)
ax.plot_surface(m1, m2, y, cmap='coolwarm')
# 梯度和源函数图像的关系
mod = np.sqrt(grad[0]**2+grad[1]**2)
mod = np.reshape(mod, m1.shape)
ax.plot_surface(m1, m2, mod)
ax.set_xlabel('x1')
ax.set_ylabel('x2')
ax.set_zlabel('f([x1,x2])')
plt.show()
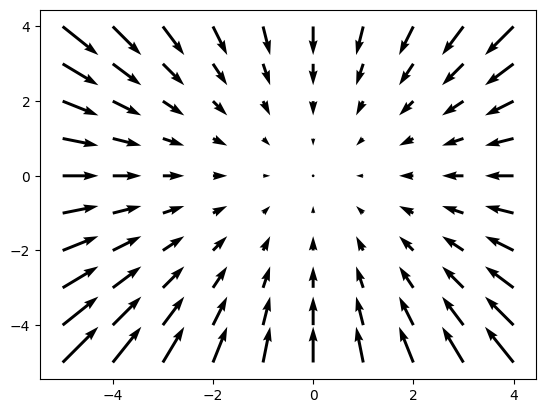
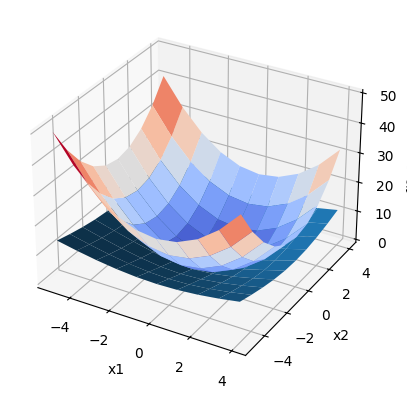
上图非常直观地显示了梯度向量和原函数之间的关系,负梯度向量指示的方向是原函数图像的最低处,离最低点越远则梯度向量的模越大。
书中讲,梯度指示的方向是各点处的函数值减小最多的方向。
梯度法
引用书中原文,
机器学习的主要任务是在学习时寻找最优参数。同样地,神经网络也必须 在学习时找到最优参数(权重和偏置)。这里所说的最优参数是指损失函数 取最小值时的参数。 一般而言,损失函数很复杂,参数空间庞大,我们不 知道它在何处能取得最小值。而通过巧妙地使用梯度来寻找函数最小值 (或者尽可能小的值)的方法就是梯度法。
...实际上,在复杂的函数中,梯度指示的方向基本上都不是函数值最小处。
...函数的极小值、最小值以及被称为鞍点(saddle point)的地方,梯度为 0。 极小值是局部最小值,也就是限定在某个范围内的最小值。 鞍点是从某个方向上看是极大值,从另一个方向上看则是极小值的点。 此外,当函数很复杂且呈扁平状时,学习可能会进入一个(几乎)平坦的地区, 陷入被称为“学习高原”的无法前进的停滞期。
利用梯度寻找使损失函数最小的参数的方法叫梯度下降法 (gradient descent method), 反之求最大就是梯度上升法 (gradient ascent method)。深度学习说梯度法一般指 梯度下降法。
上面写的函数 $f(x_1, x_2)=x_1^2+x_2^2$ 梯度下降法数学表达式:
$$ x_0 = x_0 - \eta \frac{\partial f}{\partial x_0} \ x_1 = x_1 - \eta \frac{\partial f}{\partial x_1} $$
其中 $\eta$ 是学习率,个人理解梯度向量乘上学习率,就是每次梯度下降法调整参数的方向和大小。
用 python 实现如下:
import numpy as np
import matplotlib.pyplot as plt
def f(x):
return x[0]**2+x[1]**2
def numerical_gradient(f, x):
h = 1e-4
grad = np.zeros_like(x)
for idx in range(x.size):
tmp_val = x[idx]
# f(x+h)
x[idx] = tmp_val + h
fxh1 = f(x)
# f(x-h)
x[idx] = tmp_val - h
fxh2 = f(x)
grad[idx] = (fxh1 - fxh2) / (2*h)
x[idx] = tmp_val
return grad
def gradient_descent(f, init_x, learning_rate, steps=100, optimize_history=False):
x = init_x
if optimize_history:
history = []
history.append(init_x.copy())
for _ in range(steps):
grad = numerical_gradient(f, x)
# x1 - \eta \frac{\partial f}{\partial x1}
x -= learning_rate * grad
if optimize_history:
history.append(x.copy())
if optimize_history:
return x, np.array(history)
return x
init_x = np.array([-3.0, 4.0])
lr = 0.1
step_num = 20
plt.axhline(0, linestyle=':', color='black')
plt.axvline(0, linestyle=':', color='black')
x, x_history = gradient_descent(f, init_x, lr, step_num, True)
plt.plot(x[0], x[1], '*', color='cyan')
plt.plot(x_history[:, 0], x_history[:, 1], 'o', color='blue')
plt.xlim(-3.5, 3.5)
plt.ylim(-4.5, 4.5)
plt.xlabel("X0")
plt.ylabel("X1")
plt.show()
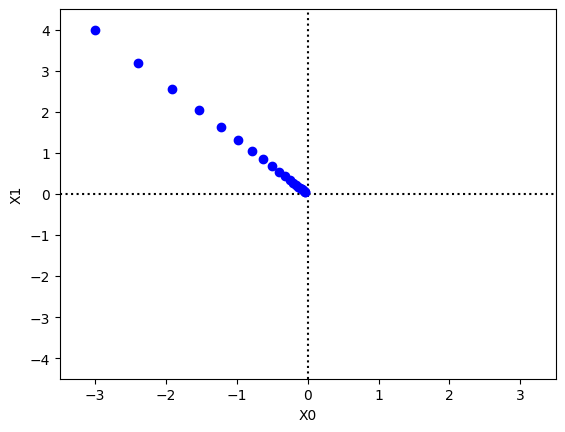
学习率过高,函数结果可能发散,书上配图很清楚了,也可以百度一下相关 loss 函数在不同学习率下结果的变化。
学习率这样的参数叫做超参数,不同于神经网络的权重,学习率这样的超参数则是人工设定的。一般超参数需要尝试多个值找到可以使学习顺利进行的设定。
神经网络学习
对神经网络采取梯度下降法优化时,梯度下降法公式这样表示:
$$ W = \begin{bmatrix} w_{11} & w_{12} & w_{13} \ w_{21} & w_{22} & w_{23} \end{bmatrix} \ \frac{\partial L}{\partial W} = \begin{bmatrix} \frac{\partial L}{\partial w_{11}} & \frac{\partial L}{\partial w_{12}} & \frac{\partial L}{\partial w_{13}} \ \frac{\partial L}{\partial w_{21}} & \frac{\partial L}{\partial w_{22}} & \frac{\partial L}{\partial w_{23}} \end{bmatrix} $$
对应的 python 实现如下:
from common import gradient, loss, activation
import sys
import numpy as np
import matplotlib.pyplot as plt
sys.path.append('..')
class simpleNet:
def __init__(self):
self.W = np.random.randn(2, 3) # 用高斯分布进行初始化
def predict(self, x):
return activation.softmax(np.dot(x, self.W))
def loss(self, x, t):
y = self.predict(x)
l = loss.cross_entropy_error(y, t)
return l
net = simpleNet()
# 输出权重
print('权重\n', net.W)
# 预测
x = np.array([0.6, 0.9])
p = net.predict(x)
t = np.array([0, 0, 1])
print('预测\n', p)
print('正解\n', t)
print('预测结果\n', np.argmax(p))
# 计算损失
print('损失\n', net.loss(x, t))
# 计算梯度
g = gradient.numerical_gradient(lambda w: net.loss(x, t), net.W)
print('梯度\n', g)
权重
[[ 0.05909374 -0.8483816 -0.16256387]
[-0.08178002 0.42475819 0.90001489]]
预测
[0.24792207 0.22690096 0.52517697]
正解
[0 0 1]
预测结果
2
损失
0.6440197935129427
梯度
[[ 0.14875321 0.13614055 -0.28489376]
[ 0.22312982 0.20421083 -0.42734064]]
至此,对梯度下降法有了基本了解,可以开始训练一个神经网络了。
对上文中 from common import 进来的几个模块,都是前面章节实现过的内容。只有 numerical_gradient 做了一些修改,主要是用了 np.nditer 多维迭代器 实现多维数组参数中迭代计算每个参数的梯度值。
2 层 MNIST 手写数字识别神经网络训练
接下来设计并训练一个具有输入层、隐藏层、输出层的神经网络用于识别手写数字。
- 输入层:100x786,batch size 设置为 100 ,输入信号 786 (28x28)
- 隐藏层:100个神经元,786个输入信号
- 输出层:10个神经元,100个输入信号
这个神经网络会参考书中这一节的例子,但主要还是根据本书前四章的内容自行编写实现。
import os
import sys
import time
from typing import Any, Callable, List, Sequence, Tuple
import numpy as np
def load_train() -> Tuple[Any, Any]:
repo_root = os.path.abspath(os.path.pardir)
if repo_root not in sys.path:
sys.path.append(repo_root)
from dataset.mnist import load_mnist
training_data, _ = load_mnist(one_hot_label=True)
return training_data
def sigmoid(a: np.ndarray) -> np.ndarray:
""" sigmoid 激活函数
"""
return 1/(1+np.exp(-a))
def softmax(a: np.ndarray) -> np.ndarray:
""" softmax 激活函数
"""
return np.exp(a)/np.sum(np.exp(a))
def cross_entropy_error(y: np.ndarray, t: np.ndarray) -> np.ndarray:
""" 交叉熵误差
"""
_delta = 0e-7 # 避免 np.log(0) 得到 -inf
return -np.sum(t*np.log(y+_delta))
def layered_numerical_gradient(f: Callable[[np.ndarray], np.ndarray], x: Sequence[np.ndarray]) -> List[np.ndarray]:
""" 分层的数值微分法计算梯度
"""
h = 1e-5
all_g = []
for layer in x:
g = np.zeros_like(layer)
it = np.nditer(layer, flags=['multi_index'], op_flags=['readwrite'])
while not it.finished:
i = it.multi_index
tmp = layer[i]
layer[i] = tmp+h
fxh1 = f(layer)
layer[i] = tmp-h
fxh2 = f(layer)
g[i] = (fxh1-fxh2)/(2*h)
layer[i] = tmp
it.iternext()
all_g.append(g)
return all_g
def predict(x: np.ndarray, w: np.ndarray, b: np.ndarray, activation: Sequence[Callable[[np.ndarray], np.ndarray]]):
""" 计算整个神经网络的输出信号
"""
if len(w) != len(b):
raise Exception(f'weights/biases shape not match: {len(w)}!={len(b)}')
if len(activation) != len(w):
raise Exception('activation function not match layer size')
for i in range(len(w)):
x = activation[i](x.dot(w[i])+b[i])
return x
# 神经网络参数
w = [np.random.randn(784, 50), np.random.randn(50, 10)]
b = [np.zeros(50), np.zeros_like(10)]
a = [sigmoid, softmax]
# 超参数
lr = 0.01
epoch = 10
batch_size = 100
# 样本和标签
x_train, t_train = load_train()
iter_num = 5
for i in range(iter_num):
_start = time.time()
# 取小批量样本
batch_mask = np.random.choice(x_train.shape[0], batch_size)
samples, labels = x_train[batch_mask], t_train[batch_mask]
# 定义预测和损失函数
def pred(_): return predict(samples, w, b, a)
def loss_w(_): return cross_entropy_error(pred(w), labels)
# 逐层计算梯度
g = layered_numerical_gradient(loss_w, w)
# 逐层微调权重参数
for layer, grad in enumerate(g):
w[layer] -= grad*lr
print(f'iter {i}, elapsed: {time.time()-_start}, loss: {loss_w(None)}')
iter 0, elapsed: 12.719797372817993, loss: 1195.7995518433572
iter 1, elapsed: 12.671370267868042, loss: 1047.1394625639487
iter 2, elapsed: 12.680177688598633, loss: 1031.436962952565
iter 3, elapsed: 12.836873292922974, loss: 852.8958334219432
iter 4, elapsed: 12.996968746185303, loss: 878.8646665014905