神经网络
具体地讲,神经网络的一个重要性质是它可以自动地从数据中学习到合适的权重参数。
神经网络
例子:
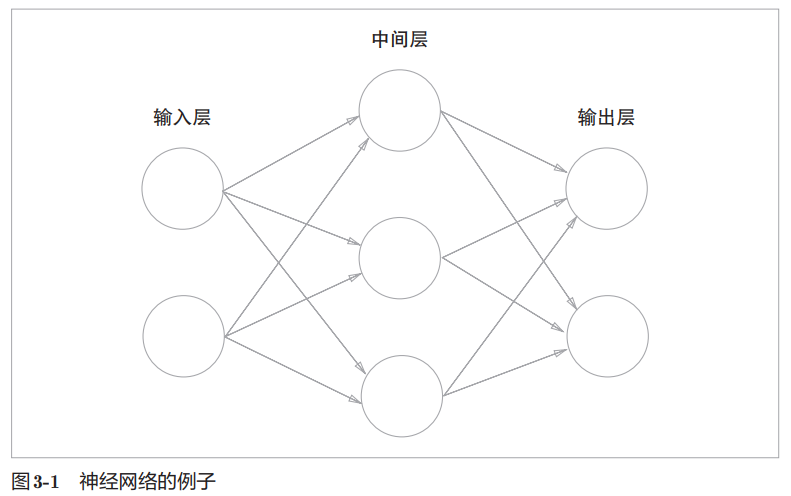
图中的神经网络共三层,其中两层有权重(隐藏层和输出层)。
按顺序分为第0层(输入层)、第1层(隐藏层)、第2层(输出层)。
这一章有个无底深坑要注意:书里明确提示,文中的 n 层神经网络,n=输入层+隐藏层+输出层-1。
在下文的神经网络实现里讲的 3 层神经网络,实际和本章开头配的图完全不一样! 下文神经网络实现一节中,实现的网络实际有一个输入层,两个隐藏层,一个输出层。
激活函数
回顾感知机的定义:
$$ y=\begin{cases} 0 & (w_1x_1 + w_2x_2 + bias \le 0) \ 1 & (w_1x_1 + w_2x_2 + bias \gt 0) \end{cases} $$
引入新的函数 $h(x)$ 来表示 $x$ 大于零时返回 1,$x$ 小于 0 返回 0 的行为,将上面的式子简化为:
$$ a = w_1x_1 + w_2x_2 + bias y = h(a) $$
$y$ 表示输出信号,$a$ 表示输入信号的加权和和偏置的总和,而 $h$ 就是所谓的激活函数。
阶跃函数
阶跃函数的定义是输入在某个阈值前后发生跳跃的函数,例如上面定义的
$$ h = \begin{cases} 0 & (a \le 0) \ 1 & (a \gt 0) \end{cases} $$
函数图像如下
import numpy as np
import matplotlib.pyplot as plt
x = np.arange(-5.0, 5.0, 0.1)
y = (x > 0).astype(np.int32)
plt.axvline(0, color='black')
plt.axhline(0, color='black')
plt.xticks(np.arange(-5.0, 5.0, 1))
plt.plot(x, y)
plt.show()
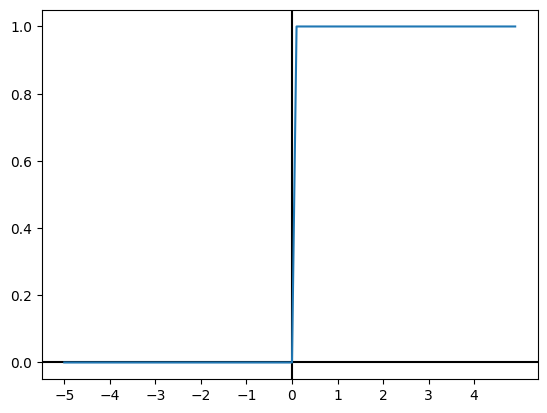
阶跃函数的值呈现阶梯状的变化,所以称为阶跃函数。
sigmoid 函数
sigmoid 函数的定义是:
$$ h(a) = \frac{1}{1 + e^{-a}} $$
函数图像如下
import numpy as np
import matplotlib.pyplot as plt
def sigmoid(x):
return 1 / (1 + np.exp(-x))
x = np.arange(-5.0, 5.0, 0.1)
y = 1 / (1 + np.exp(-x))
plt.axvline(0, color='black')
plt.axhline(0, color='black')
plt.xticks(np.arange(-5.0, 5.0, 1))
plt.plot(x, y)
plt.plot(x, sigmoid(x))
plt.show()
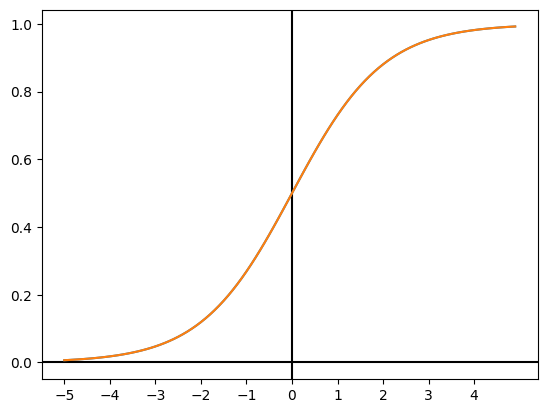
sigmoid 函数和阶跃函数的区别:
- sigmoid 函数的输出曲线是平滑的,阶跃函数的输出曲线是阶梯状的。
- sigmoid 函数的输出范围是 $x \in \mathbb{R}, 0 \le x \le 1$,阶跃函数的输出范围在 $x \in {0,1}$。
两者的相似之处:
- sigmoid 和阶跃函数在输入越是大于零,输出接近1,反之输入越小,输出越接近0。换言之,输入重要性(权重)越大,输出越大。
- 两者取值都在 $x \in \mathbb{R}, 0 \le x \le 1$ 区间。阶跃函数值域是 sigmoid 函数值域的真子集。
非线性函数
线性函数的定义是 $h(x) = cx$,其中 $c$ 是常数。高中数学知识,$h(x)$ 的函数图像是一条直线。 而非线性函数顾名思义,函数图像不是一条直线。
神经网络的激活函数必须是非线性函数,原因是线性函数做激活函数时,无论如何叠加层数,都有等效的无隐藏层神经网络。
例如,将 $h(x) = cx$ 这个函数叠加两层,得到 $h(h(x)) = c^2x$,这个函数的函数图像是一条直线,和原函数区别只在常数项不同。
依然可以等效为单层神经元,激活函数定义为 $y = ax$,其中 $a = c^2$。这样叠加多层神经网络就没有意义了。
ReLU 函数
ReLU (Rectified Linear Unit) 函数定义如下。
$$ h(a) = \max(0, a) $$
python 实现如下:
def relu(x):
return np.maximum(0, x)
函数图像如下:
import numpy as np
import matplotlib.pyplot as plt
def relu(x):
return np.maximum(0, x)
x = np.arange(-5.0, 5.0, 0.1)
y = relu(x)
plt.axvline(0, color='black')
plt.axhline(0, color='black')
plt.xticks(np.arange(-5.0, 5.0, 1))
plt.plot(x, y)
plt.show()
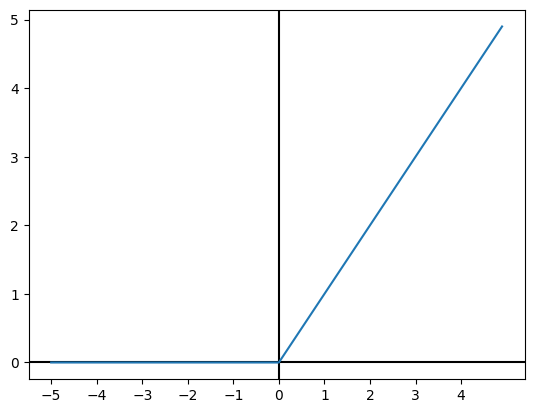
矩阵计算
ndarray 的 dot 计算的才是点积,* 运算符计算的不是。
点积的计算方式参考矩阵乘法
$$ \begin{bmatrix} a & b \ c & d \end{bmatrix} \begin{bmatrix} e & f \ g & h \end{bmatrix} = \begin{bmatrix} ae + bg & af + bh \ ce + dg & cf + dh \end{bmatrix} $$
值得注意的是矩阵点积计算是不满足交换律的,即 $A \dot B \ne B \dot A$。
要求矩阵的形状满足符号左边的x1的列数等于符号右边的x2的行数。比如说 2x3 矩阵 可以和 3x2 矩阵求点积,但不能和 2x2 矩阵求点积。
矩阵点积运算结果形状是左边矩阵的行数和右边矩阵的列数。
import numpy as np
x1 = np.array([[1, 2, 3], [4, 5, 6]])
x2 = np.array([[1, 2], [3, 4], [5, 6]])
result = x1.dot(x2)
print(result)
assert result.shape == (x1.shape[0], x2.shape[1])
[[22 28]
[49 64]]
更多关于矩阵计算内容不赘述。
矩阵乘法可以应用于神经网络层的权重参数计算。
例如设有 2 个神经元的输入层为 $x_0$ ,3 个神经元的中间层为 $x_1$,2个神经元的输出层为 $y$ 的神经网络:
$$ x_0 inputs = \begin{bmatrix} x_1 & x_2 \end{bmatrix} \ x_1 weights = \begin{bmatrix} neuro_1w_1 & neuro_2w_1 & neuro_3w_1 \ neuro_1w_2 & neuro_2w_2 & neuro_3w_2 \end{bmatrix} \ y weights = \begin{bmatrix} neuro_1w_1 & neuro_2w_1 \ neuro_1w_2 & neuro_2w_2 \ neuro_1w_3 & neuro_2w_3 \end{bmatrix} $$
$x_1$ 的矩阵含义可以这么表示。
| / | 神经元1 | 神经元2 | 神经元3 |
|---|---|---|---|
| 输入权重1 | 1.0 | 1.0 | 1.0 |
| 输入权重2 | 1.0 | 1.0 | 1.0 |
把神经元和输入权重构建出矩阵后,就可以利用矩阵乘法来计算一整个层每个神经元的输入加权和了(即$y=h(a)$中的$a$)。
批量处理神经元输入的加权和在机器学习中很重要,因为神经元的数量非常大,计算量非常大。 批量计算可以充分利用硬件加速机制比如SIMD指令或者CUDA。
inputs = np.array([[1.0, 1.0]])
weights = np.array([[0.5, 0.5, 0.5], [1.0, 1.0, 1.0]])
accumulate = inputs.dot(weights)
print(accumulate)
[[1.5 1.5 1.5]]
那么现在实现一下三层神经网络。
import numpy as np
from typing import Callable, Sequence
def identity(x: np.ndarray):
return x
def sigmoid(x: np.ndarray):
return 1 / (1 + np.exp(-x))
class Layer:
def __init__(self, name: str, weights: np.ndarray, biases: np.ndarray,
activation: Callable[[np.ndarray], np.ndarray]):
self.name = name
self.weights = weights
self.biases = biases
self.activation = activation
def evaluate(self, inputs: np.ndarray) -> np.ndarray:
return self.activation(inputs.dot(self.weights) + self.biases)
class Network:
def __init__(self, layers: Sequence[Layer]):
self.layers = layers
def evaluate(self, inputs: np.ndarray) -> np.ndarray:
for layer in self.layers:
inputs = layer.evaluate(inputs)
return inputs
layers = [
# 输入层实际就是输入的向量
# 隐藏层
Layer(
'input',
weights=np.array([[0.5, 0.5, 0.5],
[1.0, 1.0, 1.0]]),
biases=np.array([-1.0, -1.0, -1.0]),
activation=sigmoid
),
# 隐藏层
Layer(
'middle',
weights=np.array([[1.0, 1.0],
[1.0, 1.0],
[1.0, 1.0]]),
biases=np.array([-1.0, -1.0]),
activation=sigmoid
),
# 输出层
Layer(
'output',
weights=np.array([[1.0, 1.0],
[1.0, 1.0]]),
biases=np.array([-1.0, -1.0]),
activation=identity
)
]
network = Network(layers)
output = network.evaluate(np.array([[1.0, 1.0]]))
print(output)
[[0.40839964 0.40839964]]
其中有个让我很困惑的地方就是所谓的偏置单元。
偏置单元恒定输出 1 连接下一层神经网络,在前文的激活函数公式 $h(x) = wx+b$ 里以及案例代码中偏置值都是一个矩阵或np.ndarray, 但在图例中偏置值看起来是个标量常数。而我预期的是每个神经元有个独立的偏置值。
钻了几分钟的牛角尖后注意到,当偏置单元恒定输出 1 的时候,那偏置单元输出的权重其实就等于偏置值了。 所以输出层得到的输入其实是 $h(w_b+x_1w_1+x_2w_2+x_3w_3)$,其中 $w_b$ 就是偏置值。
不过实际算的时候还是套最初的加权和公式。用偏置单元来表示应该是方便后面的反向传播理解和计算。
输出层设计
神经网络可以用在分类问题和回归问题上,不过需要根据情况改变输出层的激活函数。 一般而言,回归问题用恒等函数,分类问题用softmax函数。
注:恒等函数就是上面例子代码里的
identity函数,其定义就是 $h(a) = a$。又注: 分类问题是指像前两章里学的感知机实现逻辑门,即数据属于哪个类别的问题。 回归问题则是根据输入预测一个(可能连续的)数值的问题,比如根据人的照片预测体重。
这一节引入了 softmax 函数,定义如下:
$$ softmax(a_k)=\frac{\exp(a_k)}{\sum_{i=1}^{n}\exp(a_i)} $$
其中,下标k表示输出层的第k个神经元,a_k表示第k个神经元的输入信号加权和。 exp表示e为底的指数函数,比如 $exp(3)=e^3$。 仔细看下公式会发现其实求的就是第k个神经元激活的概率,其中引入exp的原因我比较好奇搜了下, 有说是因为指数函数求导比较方便?即 $(e^x)'=e^x$。
python 实现如下:
import numpy as np
def softmax(x: np.ndarray):
return np.exp(x) / np.sum(np.exp(x))
print(softmax(np.array([0.3, 2.9, 4.0])))
[0.01821127 0.24519181 0.73659691]
然后是 softmax 的变体,softmax 的公式直接用 python 实现有个问题是指数函数的输出会爆炸, 而浮点数类型是会溢出的,溢出就会变成 inf 然后一参与计算就 nan 了。
在 numpy 的场合可以修改一下 softmax 函数,让 $exp(a_k)$ 中的 $a_k$ 减去常数 $C'$,定义为 $C'=\max(a_1,a_2,...,a_n)$, numpy 就可以保证不溢出了...吗?
注:$exp(a_k)$ 输入 $a_k$ 的最小值都会算出 inf 了,那就不是 softmax 的问题了, 可以先加个 bias 把数值巨大但数值间差异相对小的输入集合降到一个比较小的数字再处理。
公式推导如下,我懒得敲 Latex 了:
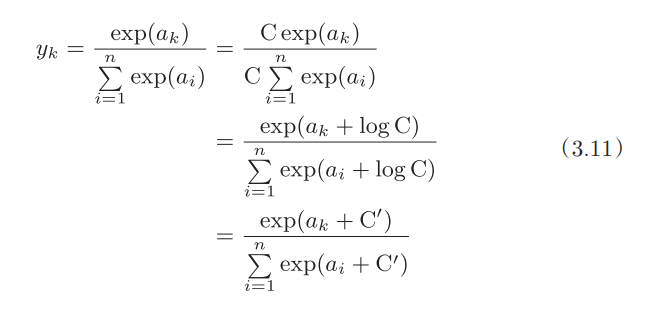
优化后的实现如下:
def softmax(x: np.ndarray):
C = np.max(x)
return np.exp(x - C) / np.sum(np.exp(x - C))
顺便吐槽一句,讲完 softmax 才提到因为要计算指数函数所以 softmax 一般在分类问题的输出层忽略以节省性能。
所以重要的还是 softmax 在训练阶段的作用。
最后是输出层的神经元数量。
分类问题中输出层神经元数量一般就是类别的数量,比如手写数字识别就有 10 个类别。
识别手写数字
mnist 真的没啥可说的,对 ai 感兴趣上手走得第一步弯路就是 import tensorflow as tf 和 mnist 数据集。
加载数据集
import sys
import os
sys.path.append(os.pardir)
import numpy as np
from matplotlib import pyplot as plt
from dataset.mnist import load_mnist
(x_train, t_train), (x_test, t_test) = load_mnist(flatten=True, normalize=False)
img = x_train[0]
label = t_train[0]
print(label) # 5
print(img.shape) # (784,)
img = img.reshape(28, 28) # 把图像的形状变成原来的尺寸
print(img.shape) # (28, 28)
plt.imshow(img)
plt.show()
5
(784,)
(28, 28)
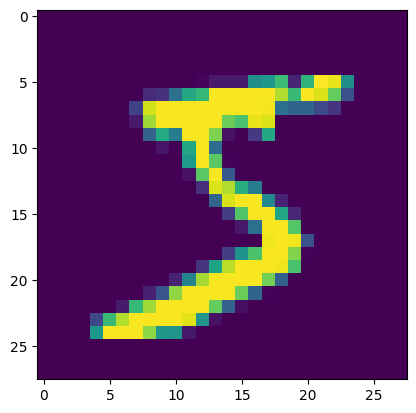
代码有几个要解释的地方。
x_train 是训练数据集,图片大小是 28x28 的灰度图,每个字节就是一个灰度值,每张图就是一个 784 长度的 numpy 数组。
t_train 是训练的标签,同一个下标对应的 x_train 就是标签对应的图片。
reshape 函数的作用是把一维的数组转换成二维的数组,比如把 784 长度的数组转换成 28x28 的二维数组。
评估神经网络
现在定义神经网络。示例的神经网络一共三层,两个隐藏层一个输出层。输入层 784 个神经元,隐藏层分别是 50 个和 100 个神经元,输出层 10 个神经元。
隐藏层神经元数量是任意的,不过我猜太少会对识别精度有影响,而超过一定数量对识别精度的帮助应该会出现边际效应递减。
需要注意的是下文示例中 load_mnist 默认使用了 normalize=True 参数,会把输入的灰度值 0~255 转成 0~1 的浮点数。
numpy.argmax 函数的作用是找到最大值的下标,用于找出神经网络输出层10个神经元中哪个下标最大(最可能是哪个数字),然后和 t_train 的标签对比,确认是否识别正确。
import pickle
import numpy as np
from typing import Callable, Sequence
class Layer:
def __init__(self, name: str, weights: np.ndarray, biases: np.ndarray,
activation: Callable[[np.ndarray], np.ndarray]):
self.name = name
self.weights = weights
self.biases = biases
self.activation = activation
def evaluate(self, inputs: np.ndarray) -> np.ndarray:
return self.activation(inputs.dot(self.weights) + self.biases)
class Network:
def __init__(self, layers: Sequence[Layer]):
self.layers = layers
def evaluate(self, inputs: np.ndarray) -> np.ndarray:
for layer in self.layers:
inputs = layer.evaluate(inputs)
return inputs
def softmax(x: np.ndarray):
C = np.max(x)
return np.exp(x - C) / np.sum(np.exp(x - C))
def sigmoid(x: np.ndarray):
return 1 / (1 + np.exp(-x))
with open('./sample_weight.pkl', 'rb') as f:
weights = pickle.load(f)
print(weights.keys())
layers = [
# 输入层略
# 隐藏层1
Layer(
name='hidden1',
weights=weights['W1'],
biases=weights['b1'],
activation=sigmoid,
),
# 隐藏层2
Layer(
name='hidden2',
weights=weights['W2'],
biases=weights['b2'],
activation=sigmoid,
),
# 输出层
Layer(
name='output',
weights=weights['W3'],
biases=weights['b3'],
activation=softmax,
),
]
network = Network(layers)
(x_train, t_train), (x_test, t_test) = load_mnist()
accuracy = 0
for i in range(len(x_train)):
if i % 1000 == 0:
percent = i/len(x_train)*100
print(f'evaluating ... %{round(percent,2)}')
y = network.evaluate(x_train[i])
p = np.argmax(y)
if p == t_train[i]:
accuracy += 1
print('accuracy: %', round(accuracy/len(x_train), 4)*100)
dict_keys(['b2', 'W1', 'b1', 'W2', 'W3', 'b3'])
evaluating ... %0.0
evaluating ... %1.67
evaluating ... %3.33
evaluating ... %5.0
evaluating ... %6.67
evaluating ... %8.33
evaluating ... %10.0
evaluating ... %11.67
evaluating ... %13.33
evaluating ... %15.0
evaluating ... %16.67
evaluating ... %18.33
evaluating ... %20.0
evaluating ... %21.67
evaluating ... %23.33
evaluating ... %25.0
evaluating ... %26.67
evaluating ... %28.33
evaluating ... %30.0
evaluating ... %31.67
evaluating ... %33.33
evaluating ... %35.0
evaluating ... %36.67
evaluating ... %38.33
evaluating ... %40.0
evaluating ... %41.67
evaluating ... %43.33
evaluating ... %45.0
evaluating ... %46.67
evaluating ... %48.33
evaluating ... %50.0
evaluating ... %51.67
evaluating ... %53.33
evaluating ... %55.0
evaluating ... %56.67
evaluating ... %58.33
evaluating ... %60.0
evaluating ... %61.67
evaluating ... %63.33
evaluating ... %65.0
evaluating ... %66.67
evaluating ... %68.33
evaluating ... %70.0
evaluating ... %71.67
evaluating ... %73.33
evaluating ... %75.0
evaluating ... %76.67
evaluating ... %78.33
evaluating ... %80.0
evaluating ... %81.67
evaluating ... %83.33
evaluating ... %85.0
evaluating ... %86.67
evaluating ... %88.33
evaluating ... %90.0
evaluating ... %91.67
evaluating ... %93.33
evaluating ... %95.0
evaluating ... %96.67
evaluating ... %98.33
accuracy: % 93.58
然后是更有趣的部分,批量化训练。
在前面的所有神经网络例子中,输入都是一维的,输出也是一维的。书中的批处理例子,则把输入改成了二维的,每行一个样本,输出也变成了二维的,一行一个结果。
不修改神经网络代码的情况下是怎么做到的呢?
还是要依赖矩阵乘法的计算法则。还记得矩阵点积定义吧?
$$ \begin{bmatrix} a & b \ c & d \end{bmatrix} \begin{bmatrix} e & f \ g & h \end{bmatrix} = \begin{bmatrix} ae + bg & af + bh \ ce + dg & cf + dh \end{bmatrix} $$
- 点积用运算符左侧矩阵的行,分别乘以运算符右侧矩阵的列。
- 点积计算结果的行数等于运算符左侧的行数,列数等于运算符右侧的列数。
神经网络的每个层,每个神经元,都有一个输入矩阵和权重矩阵,输出也是一个矩阵。当输入层输入是一维矩阵时,根据上述的定义,神经元的输入加权和总是一维的。
w 的下标对应的是输入信号的下标(运算符左侧矩阵的列号),上标是神经元的序号。 下面的公式中 a 的下标是输入样本的索引(运算符左侧矩阵的行号),上标是神经元的序号。
$$ \begin{bmatrix} x_1 & x_2 & x_3 \end{bmatrix} \begin{bmatrix} w_{1}^{1} & w_{1}^{2} & w_{1}^{3} \ w_{2}^{1} & w_{2}^{2} & w_{2}^{3} \ w_{3}^{1} & w_{3}^{2} & w_{3}^{3} \end{bmatrix}= \begin{bmatrix} a_{1}^{1} & a_{1}^{2} & a_{1}^{2} \end{bmatrix} $$
而神经元的输出不会改变输入加权和矩阵的形状。
$$ activation(\begin{bmatrix} a_1^1 & a_1^2 & a_1^3 \end{bmatrix})= \begin{bmatrix} y_1^1 & y_1^2 & y_1^3 \end{bmatrix} $$
而神经元输出会作为下一个神经元的输入,于是信号矩阵在神经网络层之间传递时,只有列数会发生变更,行数总是和输入一致的。
因此当输入是多维的时候,最终输出层输出的结果矩阵,总是和输入层的矩阵行数一致。
我们实际试一下。
import pickle
import numpy as np
from typing import Callable, Sequence
class Layer:
def __init__(self, name: str, weights: np.ndarray, biases: np.ndarray,
activation: Callable[[np.ndarray], np.ndarray]):
self.name = name
self.weights = weights
self.biases = biases
self.activation = activation
def evaluate(self, inputs: np.ndarray) -> np.ndarray:
return self.activation(inputs.dot(self.weights) + self.biases)
class Network:
def __init__(self, layers: Sequence[Layer]):
self.layers = layers
def evaluate(self, inputs: np.ndarray) -> np.ndarray:
for layer in self.layers:
inputs = layer.evaluate(inputs)
return inputs
def softmax(x: np.ndarray):
C = np.max(x)
return np.exp(x - C) / np.sum(np.exp(x - C))
def sigmoid(x: np.ndarray):
return 1 / (1 + np.exp(-x))
with open('./sample_weight.pkl', 'rb') as f:
weights = pickle.load(f)
print(weights.keys())
layers = [
# 输入层略
# 隐藏层1
Layer(
name='hidden1',
weights=weights['W1'],
biases=weights['b1'],
activation=sigmoid,
),
# 隐藏层2
Layer(
name='hidden2',
weights=weights['W2'],
biases=weights['b2'],
activation=sigmoid,
),
# 输出层
Layer(
name='output',
weights=weights['W3'],
biases=weights['b3'],
activation=softmax,
),
]
network = Network(layers)
(x_train, t_train), (x_test, t_test) = load_mnist()
accuracy = 0
batch_size=100
for i in range(0,len(x_train),batch_size):
if i % 1000 == 0:
percent = i/len(x_train)*100
print(f'evaluating ... %{round(percent,2)}')
y = network.evaluate(x_train[i:i+batch_size])
p = np.argmax(y, axis=1) # 取每一行的最大值下标
accuracy += np.sum(p == t_train[i:i+batch_size])
print('accuracy: %', round(accuracy/len(x_train), 4)*100)
dict_keys(['b2', 'W1', 'b1', 'W2', 'W3', 'b3'])
evaluating ... %0.0
evaluating ... %1.67
evaluating ... %3.33
evaluating ... %5.0
evaluating ... %6.67
evaluating ... %8.33
evaluating ... %10.0
evaluating ... %11.67
evaluating ... %13.33
evaluating ... %15.0
evaluating ... %16.67
evaluating ... %18.33
evaluating ... %20.0
evaluating ... %21.67
evaluating ... %23.33
evaluating ... %25.0
evaluating ... %26.67
evaluating ... %28.33
evaluating ... %30.0
evaluating ... %31.67
evaluating ... %33.33
evaluating ... %35.0
evaluating ... %36.67
evaluating ... %38.33
evaluating ... %40.0
evaluating ... %41.67
evaluating ... %43.33
evaluating ... %45.0
evaluating ... %46.67
evaluating ... %48.33
evaluating ... %50.0
evaluating ... %51.67
evaluating ... %53.33
evaluating ... %55.0
evaluating ... %56.67
evaluating ... %58.33
evaluating ... %60.0
evaluating ... %61.67
evaluating ... %63.33
evaluating ... %65.0
evaluating ... %66.67
evaluating ... %68.33
evaluating ... %70.0
evaluating ... %71.67
evaluating ... %73.33
evaluating ... %75.0
evaluating ... %76.67
evaluating ... %78.33
evaluating ... %80.0
evaluating ... %81.67
evaluating ... %83.33
evaluating ... %85.0
evaluating ... %86.67
evaluating ... %88.33
evaluating ... %90.0
evaluating ... %91.67
evaluating ... %93.33
evaluating ... %95.0
evaluating ... %96.67
evaluating ... %98.33
accuracy: % 93.58
我的机器上实测到的结果是,100个样本一批处理,训练集执行只花了0.3秒。一个一个处理则花费了7秒左右。
可以说批量化加速的效果是很明显的。